東大多浪体験記 1 プロローグ

はじめに

はじめましての方ははじめまして。 そうでない方はお久しぶりです。
突然ですが、私は2018年現在、東京大学の学部3年生で、二浪して東大に入ったため「東大多浪交流会」という、サークルもどきに所属しております。(詳細については掲載記事貼っときます↓)

UmeeTにおいて、東大多浪交流会の記事が掲載されました。https://t。co/P5C1WRlL5y

— 東京大学多浪交流会(TTK) (@uT_ARO) 2017年7月25日

東大多浪交流会は、高校卒業から東大の前期教養に入学するまでに2年以上の間隔が空いてるものたちが集まっている集団で、昨年の発足から駒場祭という東大の学園祭で「東大多浪」という、多浪体験記を出版しています。 昨年、自分も執筆したのですが、字数制限と締め切りという時間制限から、「東大多浪」では満足に記すことができませんでした。
締め切りに関しては、もっと余裕持って執筆していれば良かっただけと言われればそうなので、責任転嫁と言われれば反論できませんが。
そこで、今年の「東大多浪」が発売され終えた2018年駒場祭の終了後、このブログで自分の思う存分、体験談を記そうと思ったのがことの発端です。

....という文章が、ブログの下書き欄に残ってました。構想してから１年間書いてなかったんですね、恐ろしい。自分のルーズさと時の経つ早さが。
というわけで、今回は、前々からやろうと思っていた(が恐ろしいルーズさによってやらないでいた)、多浪体験談(とできれば、その後の大学生活の少し)を綴って行きたいと思っています。

これは、高校三年生のとき、東大を志望しながらも、全国模試の偏差値は40で全ての大学に足切り(センター試験の点数が悪いために、二次試験を受ける前の段階で不合格となること)され、どこの大学も受けられずにいた受験生が、その壁の高さに心を何度も折られながらも、受験勉強の研究やメンタルコントロール術などを駆使して、奇跡的に2浪で東大に合格した物語のような体験談です。(１年前の僕談)
欲を言えば、受験生や、無謀な挑戦に向けて頑張ってる人の励みに、無謀な挑戦に頑張ってた人の慰みになれば、望外の喜びです。(１年前の僕談)

1とナンバリング打っていることから予想できる通り、いくつかの記事に分けて語っていきたいと思います。
完結まで、どれぐらいの期間を要するかわかりませんが、ゆるりと書いていこうかなと思ってます。

スタート地点をどこからにしようかと思っていたのですが、多浪交流会の冊子「東大多浪」と同じ幼少期からゆるりとはじめたいと思います。

...あ、正直、今回のやつは多浪と全く関係ないので、僕の生い立ちとか興味のない人は今回の記事はスキップして大丈夫だと思います。
続きがちゃんと出るかは不確定ですが、いつかきっと、おそらく、多分、maybe、出ると思います。

では、東大多浪体験記の始まり始まり。

2019年夏に見たアニメの総評

はじめに

まあ, こんな感じで見たアニメの感想？というか, 自分的な格付けを残しておいてもいいかもなあ, と思い投稿.
ってな訳で, この夏(?)に見たアニメのランクづけでもしていきたいと思います.
誰得な記事. もちろん, 俺得.

東京大学院試体験記

はじめに

お久しぶりです. 3ヶ月ぶりぐらいの記事です. ほんとお久しぶりですね.
これだけ 記事の間隔が空いたのは, 他でもなく, 学会の論文投稿と院試があったからです.

というわけで, 軽く院試の感想をつらつらと書いて行きたいと思います.
人生で何度もあることではないのでね.
口述試験で聞かれたことも書いたので, 気になる人はそれだけでもどうぞ.

ちなみに, 自分は, 東京大学計数工学科システム情報工学コースの4年生です.

結果

はじめに結果から書いてしまうと, 以下２つの専攻を受け, 以下のような合否結果でした

• 東京大学大学院情報理工学系システム情報学専攻...合格
• 東京大学大学院新領域創成科学研究科複雑理工専攻...合格

どっちも第一志望の教員で合格しました.
(まあ, 合格してなかったら感想記事かけるようなメンタルないから当然.)
本当は合格した研究室込みで記事を書きたいのですが(研究室によって合格の難易度が変わりうるため), そこまですると特定されかねないので勘弁してください.

感想

さて, ここから感想を書いて行きたいと思います.

【TouchDesigner】Arduinoでシリアル出力されたカンマ区切りの2つの値をTouchDesignerでグラフにする

始めに

お久しぶりです。ほんとお久しぶりです。なるみやです。
ラボの先輩がTouchDesignerででもを作っていて楽しそうだったので、バイトでTouchDesignerを使い始めて見たところ、日本語記事が少ない！！！
ただ、Arduinoから、センサでとった2つの値をTouchDesignerでグラフにしようとしたのですが、1つの値を表示するのと同じ手順でやってもできなかった...。
調べても日本語記事なかった...。解決するのに20分ぐらいかかった。というわけでブログに書き起こしました。 ちなみに、TouchDesignerの知識はほぼ0です。

1つ値シリアル出力の値をグラフにするやり方

これを参考にしてできます
→ TouchDesigner + Arduino + MAX30105 で心電図！

手順としては

1. Arduino連携しシリアルデータ取得
   ...DAT (Data)タブからSerialオペレータを選択・配置してArduinoからのシリアルデータを取得
2. シリアルデータの選択
   ...DATタブからSelectオペレータを選択・配置してSerialオペレータと結線して最新のシリアルデータのみを取得するようにする
3. 最新シリアルデータをCHOPデータに変換
   ...CHOP (Channel Operators)タブからDAT toオペレータを選択・配置してDAT値のシリアルデータをCHOP用の値に変換
4. CHOPデータをプロット
   ...CHOPタブからTrailオペレータを選択・配置してCHOPオペレータ出力と結線してデータをプロット

これでできます

2つの値を同じグラフにプロットする

本題です
手順は以下のよう

1. Arduino連携しシリアルデータ取得
   ...DAT (Data)タブからSerialオペレータを選択・配置してArduinoからのシリアルデータを取得。この時点で1つの行の値はカンマ区切りで、2つの値が格納されている

   

   こんな感じ

2. カンマ区切りの値をtebleに変換
   ...DATタブのconvertオペレーターを用いて、先のArduinoからシリアル出力された値をtableにします。Howは"To Table"に、Split Cell atは","に。

   

   tableにconvert

3. tableから値を各々選択(データの選択)
   ...selectオペレーターを使います。画像のように、Start Col IndexとEnd Col Indexをいじってあげるといいです。

4. 各々の最新シリアルデータをCHOPデータに変換...1つの値を描画するときと同じなので説明略

5. 2つのCHOPデータをプロット
   ...2つのCHOPデータをTrailオペレータに結線する

Arduinoを動かしてないですが、完成図が以下のよう。

できた！！やった！！！

最後に

TouchDesigner全くプログラム書かずにできることが多いのでいいですが、その分、やりたい！と思ったことでもオペーレーターがないとできなかったりして手枷足枷をはめてる感もありますね。使いこなしてきたら、そんなことも無くなるのでしょうか？
何より日本語文献が少ない！！！英語読め！！！！！

というわけで、久しぶりの更新でした。ほんとお久しぶりです。
なんかずっと更新してませんでした。

最近、Scrapbox使い始めて、メモとりはじめたので、今後投稿頻度が高くなるといいですね。(他人事)
てか、そろそろ、多浪体験記を書いていきたいですね。

ブログねー、いざ書こうとするとめんどくせえもん！！！
ほどほどに続けて行けたらいいですね。

【領域図示】2変数陰関数不等式の領域を図示する【Python + matplotlib】

はじめに

数値解析のレポートで、修正オイラー法や、4次のルンゲクッタ法の安定領域の図示にかなり時間食われたので、今後そんなことが無いようにここに書き残して置くことにしました。

やりたいこと

今回自分がやりたかったことは、修正オイラー法の安定条件である

$$ \left|1+ \lambda h+ \frac{(\lambda h)^2}{2}\right| < 1 \hspace{0.4cm} \lambda h \in \mathbb{C}　\tag{1} $$ や4次のルンゲクッタ法の安定条件である $$ \left|1+ \lambda h+ \frac{(\lambda h)^2}{2} + \frac{(\lambda h)^3}{6} + \frac{(\lambda h)^4}{24}\right| < 1 \hspace{0.4cm} \lambda h \in \mathbb{C} \tag{2} $$

の領域を図示することでした。
ちなみに、以下では$z= \lambda h=x+iy \, \, x,y \in \mathbb{R}$として表して行きます。

できたこと

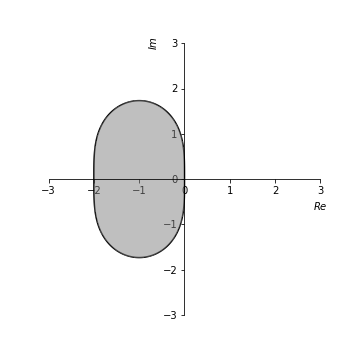
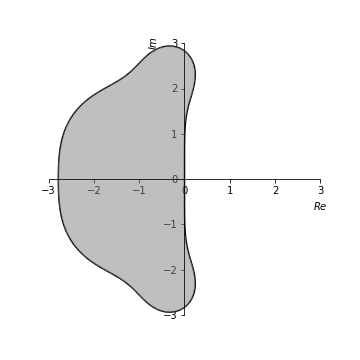
式(1)や式(2)から下の図が出来上がりました。
(1)が左で、(2)が右です。

図1.安定領域のプロット:修正オイラー法(ホイン法)(左)とルンゲクッタ法(右)

手順

式(1)や(2)の領域を図示するには以下のような方法で行きます。

1. 必要なライブラリのインポート
2. 式(1)や(2)式の両辺を2乗して整理した式を$x,y$の条件式$f(x,y) < 0$として求める
3. 手順2で求まった、陰関数型の条件$f(x,y) < 0$に対して図をプロットする

では、わかりやすいように、まず、式(1)から見て行きましょう。

実行環境はJupyterです。

手順1. 必要なライブラリのインポート

インポートしましょう

import matplotlib.pyplot as plt
import numpy as np
import matplotlib
matplotlib.use('Agg')
%matplotlib inline

from sympy import *

手順2. 両辺を2乗して整理した式を$x,y$の条件式$f(x,y) < 0$として求める

Sympyのシンボリックと、expand機能を使います。
細かいとことや、他のことが知りたい人はここをみるといいと思います。
実際のコードは以下のようになります。

x = Symbol('x', real=True) # xを実数のシンボリックと定義
y = Symbol('y', real=True) # yを実数のシンボリックと定義
z = Symbol('z') # zをシンボリックと定義

## z = x+iyと定義する　##
z = x + y*I

expr = 1 + z + (z**2)/2 # 修正オイラー法の安定条件の絶対値の中の式を変数定義
expr2 = expand(expr_z.conjugate()*expr_z) -1　# 修正オイラー法の安定条件の(左辺)^2-(右辺)^2を計算して展開
print(expr2)

これの出力は以下のようになりました。

x**4/4 + x**3 + x**2*y**2/2 + 2*x**2 + x*y**2 + 2*x + y**4/4

これで、

$$ f(x,y) = \frac{x^4}{4} + \frac{x^2 y^2}{2}+ \frac{y^4}{4} + x^3 + xy^2 + 2x^2 + 2x $$

とすることで、両辺を2乗して整理した式を$x,y$の条件式$f(x,y) < 0$として求めることができました。

手順3.手順eで求まった、陰関数型の条件$f(x,y) < 0$に対して図をプロットする

さて手順2で$f(x,y) < 0$という形までできたので、この陰関数表示されている領域をプロットします。
実際のコードは以下のようです。細かい説明はあとでします。

## プロットする領域を定める ##
max_range = 3
delta = 0.025 # 刻み幅
xrange = np.arange(-max_range, max_range, delta)
yrange = np.arange(-max_range, max_range, delta)
X, Y = np.meshgrid(xrange,yrange)

## Figureを作成 ##
fig = plt.figure(figsize=(5, 5))
# FigureにAxes(サブプロット)を追加
ax = fig.add_subplot(111)

## 軸の設定 ##
plt.axis([-max_range, max_range, -max_range, max_range])
plt.gca().set_aspect('equal', adjustable='box')


## 軸を中心の方に持っていく ##
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

## 軸にラベルをつける ##
ax.set_ylabel("$Im$",y = 1)
ax.set_xlabel("$Re$", x=1)

## 描画 ##
Z=(X**4)/4+(X**2)*(Y**2)/2 + (Y**4)/4 + X**3 + X*Y**2 + 2*X**2 + 2*X
plt.contour(X, Y, Z, [0], colors='black', corner_mask=True) # 境界線をプロット
plt.plot(X[Z < 0], Y[Z<0], color='gray',alpha=0.5) # 内部をgrayで塗る

## グラフを保存 ##
plt.savefig("./figure/heun_stb.png")  # figureディレクトリがないとエラーになるのでその時はfigureディレクトリを作ってあげること
plt.show()

これで次の図ができます。

図2.生成された図

それでは各行の説明をして行きます。

プロットする領域を定める

max_range = 3
delta = 0.025 # 刻み幅
xrange = np.arange(-max_range, max_range, delta)
yrange = np.arange(-max_range, max_range, delta)
X, Y = np.meshgrid(xrange,yrange)

この5行は、描画する範囲を決めて、その範囲内で、xrangeとyrangeというdelta刻みの配列を作って、それを格子状に貼った二個の変数X,Yをnumpy.meshgridによって生成しています。

軸の設定

## 軸の設定 ##
plt.axis([-max_range, max_range, -max_range, max_range])
plt.gca().set_aspect('equal', adjustable='box')


## 軸を中心の方に持っていく ##
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

## 軸にラベルをつける ##
ax.set_ylabel("$Im$",y = 1)
ax.set_xlabel("$Re$", x=1)

コメントの通り、軸の表示範囲と、軸の表示場所、そして、軸のラベルの設定などをしています。細かいことは、公式リファレンスへGO！()

境界線と境界線内部領域の描画

さて、ここが本題です。

#描画
Z=(X**4)/4+(X**2)*(Y**2)/2 + (Y**4)/4 + X**3 + X*Y**2 + 2*X**2 + 2*X
plt.contour(X, Y, Z, [0], colors='black', corner_mask=True)
plt.plot(X[Z < 0], Y[Z<0], color='gray',alpha=0.5)

まず、手順2で求められた$f(x,y)$の$x$を$X$に$y$を$Y$にしたものを$Z$に代入しておきます。それが1行目のコードです。
次に、どちらが先でもいいんですが、境界線の描画からして行きます。もちろんこれがなくてもいいんですが、あったほうが「それっぽい」。陰関数の境界線は、matplotlib.pyplotのcontourメソッドを用いて書きます。これはもともと、標高線をかくものみたいです。
例えば、

plt.contour(X, Y, Z, [0], colors='black', corner_mask=True)

とすると、Zの値が0となる境界線を引いてくれるらしいです。ちなみに、

plt.contour(X, Y, Z, [0,1,-1], colors='black', corner_mask=True)

とかすると、Zの値が0と-1と1の境界線を引いてくれる。colors='black'を指定しなければ、標高せんの色はカラフルになります。corner_maskはなんでTrueにしたのか覚えてないです！w

そして、境界線内部をプロットして行きます。3行目ですね。

plt.plot(X[Z < 0], Y[Z<0], color='gray',alpha=0.5)

これには普通に、Z< 0という条件のもと生成されたnumpyのboolean配列を用いて作られたX,Yの部分配列をgrayでプロットしていくだけです。
下の軸が見えるようにalpha=0.5とすることで透明度をあげてます。

最後に保存する

plt.savefig("./figure/heun_stb.png")  
plt.show()

保存します。
なお、このパス指定だと、figureディレクトリがないとエラー吐かれますので、その時は大人しく、figureディレクトリを作りましょう。もちろん、保存先先のパスを変えてもいいです。

以上！

ルンゲクッタ法の安定領域にも同じことをしてみる

手順2.$f(x,y)<0$の形にする

$f(x,y)<0$の形にするために、$f(x,y)$を求めます。

from sympy import *

x = Symbol('x', real=True)
y = Symbol('y', real=True)
z = Symbol('z')

z = x + y*I

expr_rk4 = 1 + z + (z**2)/2 + (z**3)/6  + (z**4)/24
expr_rk4_power2 = sy.expand(expr_rk4.conjugate()*expr_rk4) -1
print(expr_rk4_power2)

出力は

x**8/576 + x**7/72 + x**6*y**2/144 + 5*x**6/72 + x**5*y**2/24 + x**5/4 + x**4*y**4/96 + x**4*y**2/8 + 2*x**4/3 + x**3*y**4/24 + x**3*y**2/6 + 4*x**3/3 + x**2*y**6/144 + x**2*y**4/24 + 2*x**2 + x*y**6/72 - x*y**4/12 + 2*x + y**8/576 - y**6/72
-31/36

でした。

$$ \begin{align} f(x,y) = \frac{x^8}{576} &+ \frac{x^7}{72} + \frac{x^6 y^2}{144} + \frac{5x^6}{72} + \frac{x^5 y^2}{24} + \frac{x^5}{4} + \frac{x^4 y^4}{96} + \frac{x^4 y^2}{8} + \frac{2x^4}{3} +\frac{x^3 y^4}{24} \\ & + \frac{x^3 y^2}{6} + \frac{4^3}{3} + \frac{x^2 y^6}{144} + \frac{x^2 y^4}{24} + 2x^2 + \frac{xy^6}{72} - \frac{xy^4}{12} + 2x + \frac{y^8}{576} - \frac{y^6}{72} < 0 \end{align} $$

ですね。これは手計算で求めたくねえ。。。

手順3.図示

max_range = 3
delta = 0.025
xrange = np.arange(-max_range, max_range, delta)
yrange = np.arange(-max_range, max_range, delta)
X, Y = np.meshgrid(xrange,yrange)

# Figureを作成
fig = plt.figure(figsize=(5, 5))
# FigureにAxes(サブプロット)を追加
ax = fig.add_subplot(111)

#軸の設定
plt.axis([-max_range, max_range, -max_range, max_range])
plt.gca().set_aspect('equal', adjustable='box')

# 軸を中心の方に持っていく
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))

ax.set_ylabel("$Im$",y = 1)
ax.set_xlabel("$Re$", x=1)

#描画
Z2 = (X**8)/576 + (X**7)/72 + (X**6)*(Y**2)/144 + 5*(X**6)/72 + (X**5)*(Y**2)/24 + (X**5)/4 + (X**4)*(Y**4)/96 + (X**4)*(Y**2)/8 + 2*(X**4)/3 + (X**3)*(Y**4)/24 + (X**3)*(Y**2)/6 + 4*(X**3)/3 + (X**2)*(Y**6)/144 + (X**2)*(Y**4)/24 + 2*(X**2) + X*(Y**6)/72 - X*(Y**4)/12 + 2*X + (Y**8)/576 - (Y**6)/72

plt.contour(X, Y, Z2, [0], colors='black', corner_mask=True)
plt.plot(X[Z2 < 0], Y[Z2<0], color='gray' ,alpha=0.5)
plt.savefig("./figure/rk4_stb.png")
plt.show()

出力は

図3.出力されたルンゲクッタ法の安定領域

ちゃんとできました。
まあ、この方法、$f(x,y)<0$にした後に、Zに直接、$f(x,y)$を入力してるのすごい脳筋な方法なんですけどね。
でも変に考えずに、こっちの方が早かったので...。アホなので。

最後に

珍しく連投となりましたが、これは早く片付けたかったので、連投も構わず、連投しました連投。
さて、数値解析のレポートも終わったし、試験勉強と、もう一つのレポートしなきゃ。まずい...！！！
俺ガイルも読みたいのじゃ〜。

では今日はここまで。

参考

• Python, SymPyの使い方（因数分解、方程式、微分積分など）
• pythonで陰関数を描画
• 数値計算の安定性: Stability