【領域図示】2変数陰関数不等式の領域を図示する【Python + matplotlib】
はじめに
数値解析のレポートで、修正オイラー法や、4次のルンゲクッタ法の安定領域の図示にかなり時間食われたので、今後そんなことが無いようにここに書き残して置くことにしました。
やりたいこと
今回自分がやりたかったことは、修正オイラー法の安定条件である
$$
\left|1+ \lambda h+ \frac{(\lambda h)^2}{2}\right| < 1 \hspace{0.4cm} \lambda h \in \mathbb{C} \tag{1}
$$
や4次のルンゲクッタ法の安定条件である
$$
\left|1+ \lambda h+ \frac{(\lambda h)^2}{2} + \frac{(\lambda h)^3}{6} + \frac{(\lambda h)^4}{24}\right| < 1 \hspace{0.4cm} \lambda h \in \mathbb{C} \tag{2}
$$
の領域を図示することでした。
ちなみに、以下では$z= \lambda h=x+iy \, \, x,y \in \mathbb{R}$として表して行きます。
できたこと
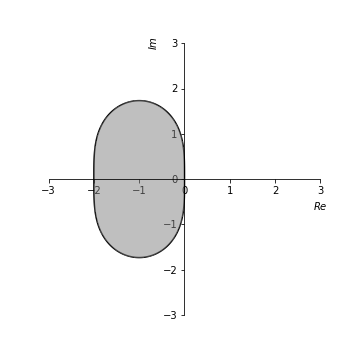
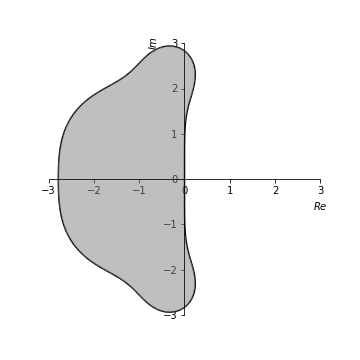
式(1)や式(2)から下の図が出来上がりました。
(1)が左で、(2)が右です。
手順
式(1)や(2)の領域を図示するには以下のような方法で行きます。
- 必要なライブラリのインポート
- 式(1)や(2)式の両辺を2乗して整理した式を$x,y$の条件式$f(x,y) < 0$として求める
- 手順2で求まった、陰関数型の条件$f(x,y) < 0$に対して図をプロットする
では、わかりやすいように、まず、式(1)から見て行きましょう。
実行環境はJupyterです。
手順1. 必要なライブラリのインポート
インポートしましょう
import matplotlib.pyplot as plt
import numpy as np
import matplotlib
matplotlib.use('Agg')
%matplotlib inline
from sympy import *
手順2. 両辺を2乗して整理した式を$x,y$の条件式$f(x,y) < 0$として求める
Sympyのシンボリックと、expand機能を使います。
細かいとことや、他のことが知りたい人はここをみるといいと思います。
実際のコードは以下のようになります。
x = Symbol('x', real=True) # xを実数のシンボリックと定義
y = Symbol('y', real=True) # yを実数のシンボリックと定義
z = Symbol('z') # zをシンボリックと定義
## z = x+iyと定義する ##
z = x + y*I
expr = 1 + z + (z**2)/2 # 修正オイラー法の安定条件の絶対値の中の式を変数定義
expr2 = expand(expr_z.conjugate()*expr_z) -1 # 修正オイラー法の安定条件の(左辺)^2-(右辺)^2を計算して展開
print(expr2)
これの出力は以下のようになりました。
x**4/4 + x**3 + x**2*y**2/2 + 2*x**2 + x*y**2 + 2*x + y**4/4
これで、
$$
f(x,y) = \frac{x^4}{4} + \frac{x^2 y^2}{2}+ \frac{y^4}{4} + x^3 + xy^2 + 2x^2 + 2x
$$
とすることで、両辺を2乗して整理した式を$x,y$の条件式$f(x,y) < 0$として求めることができました。
手順3.手順eで求まった、陰関数型の条件$f(x,y) < 0$に対して図をプロットする
さて手順2で$f(x,y) < 0$という形までできたので、この陰関数表示されている領域をプロットします。
実際のコードは以下のようです。細かい説明はあとでします。
## プロットする領域を定める ##
max_range = 3
delta = 0.025 # 刻み幅
xrange = np.arange(-max_range, max_range, delta)
yrange = np.arange(-max_range, max_range, delta)
X, Y = np.meshgrid(xrange,yrange)
## Figureを作成 ##
fig = plt.figure(figsize=(5, 5))
# FigureにAxes(サブプロット)を追加
ax = fig.add_subplot(111)
## 軸の設定 ##
plt.axis([-max_range, max_range, -max_range, max_range])
plt.gca().set_aspect('equal', adjustable='box')
## 軸を中心の方に持っていく ##
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
## 軸にラベルをつける ##
ax.set_ylabel("$Im$",y = 1)
ax.set_xlabel("$Re$", x=1)
## 描画 ##
Z=(X**4)/4+(X**2)*(Y**2)/2 + (Y**4)/4 + X**3 + X*Y**2 + 2*X**2 + 2*X
plt.contour(X, Y, Z, [0], colors='black', corner_mask=True) # 境界線をプロット
plt.plot(X[Z < 0], Y[Z<0], color='gray',alpha=0.5) # 内部をgrayで塗る
## グラフを保存 ##
plt.savefig("./figure/heun_stb.png") # figureディレクトリがないとエラーになるのでその時はfigureディレクトリを作ってあげること
plt.show()
これで次の図ができます。
それでは各行の説明をして行きます。
プロットする領域を定める
max_range = 3 delta = 0.025 # 刻み幅 xrange = np.arange(-max_range, max_range, delta) yrange = np.arange(-max_range, max_range, delta) X, Y = np.meshgrid(xrange,yrange)
この5行は、描画する範囲を決めて、その範囲内で、xrangeとyrangeというdelta刻みの配列を作って、それを格子状に貼った二個の変数X,Yをnumpy.meshgridによって生成しています。
軸の設定
## 軸の設定 ##
plt.axis([-max_range, max_range, -max_range, max_range])
plt.gca().set_aspect('equal', adjustable='box')
## 軸を中心の方に持っていく ##
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
## 軸にラベルをつける ##
ax.set_ylabel("$Im$",y = 1)
ax.set_xlabel("$Re$", x=1)
コメントの通り、軸の表示範囲と、軸の表示場所、そして、軸のラベルの設定などをしています。細かいことは、公式リファレンスへGO！()
境界線と境界線内部領域の描画
さて、ここが本題です。
#描画 Z=(X**4)/4+(X**2)*(Y**2)/2 + (Y**4)/4 + X**3 + X*Y**2 + 2*X**2 + 2*X plt.contour(X, Y, Z, [0], colors='black', corner_mask=True) plt.plot(X[Z < 0], Y[Z<0], color='gray',alpha=0.5)
まず、手順2で求められた$f(x,y)$の$x$を$X$に$y$を$Y$にしたものを$Z$に代入しておきます。それが1行目のコードです。
次に、どちらが先でもいいんですが、境界線の描画からして行きます。もちろんこれがなくてもいいんですが、あったほうが「それっぽい」。陰関数の境界線は、matplotlib.pyplotのcontourメソッドを用いて書きます。これはもともと、標高線をかくものみたいです。
例えば、
plt.contour(X, Y, Z, [0], colors='black', corner_mask=True)
とすると、Zの値が0となる境界線を引いてくれるらしいです。ちなみに、
plt.contour(X, Y, Z, [0,1,-1], colors='black', corner_mask=True)
とかすると、Zの値が0と-1と1の境界線を引いてくれる。colors='black'を指定しなければ、標高せんの色はカラフルになります。corner_maskはなんでTrueにしたのか覚えてないです！w
そして、境界線内部をプロットして行きます。3行目ですね。
plt.plot(X[Z < 0], Y[Z<0], color='gray',alpha=0.5)
これには普通に、Z< 0という条件のもと生成されたnumpyのboolean配列を用いて作られたX,Yの部分配列をgrayでプロットしていくだけです。
下の軸が見えるようにalpha=0.5とすることで透明度をあげてます。
最後に保存する
plt.savefig("./figure/heun_stb.png")
plt.show()
保存します。
なお、このパス指定だと、figureディレクトリがないとエラー吐かれますので、その時は大人しく、figureディレクトリを作りましょう。もちろん、保存先先のパスを変えてもいいです。
以上！
ルンゲクッタ法の安定領域にも同じことをしてみる
手順2.$f(x,y)<0$の形にする
$f(x,y)<0$の形にするために、$f(x,y)$を求めます。
from sympy import *
x = Symbol('x', real=True)
y = Symbol('y', real=True)
z = Symbol('z')
z = x + y*I
expr_rk4 = 1 + z + (z**2)/2 + (z**3)/6 + (z**4)/24
expr_rk4_power2 = sy.expand(expr_rk4.conjugate()*expr_rk4) -1
print(expr_rk4_power2)
出力は
x**8/576 + x**7/72 + x**6*y**2/144 + 5*x**6/72 + x**5*y**2/24 + x**5/4 + x**4*y**4/96 + x**4*y**2/8 + 2*x**4/3 + x**3*y**4/24 + x**3*y**2/6 + 4*x**3/3 + x**2*y**6/144 + x**2*y**4/24 + 2*x**2 + x*y**6/72 - x*y**4/12 + 2*x + y**8/576 - y**6/72 -31/36
でした。
$$
\begin{align}
f(x,y) = \frac{x^8}{576} &+ \frac{x^7}{72} + \frac{x^6 y^2}{144} + \frac{5x^6}{72} + \frac{x^5 y^2}{24} + \frac{x^5}{4} + \frac{x^4 y^4}{96} + \frac{x^4 y^2}{8} + \frac{2x^4}{3} +\frac{x^3 y^4}{24} \\
& + \frac{x^3 y^2}{6} + \frac{4^3}{3} + \frac{x^2 y^6}{144} + \frac{x^2 y^4}{24} + 2x^2 + \frac{xy^6}{72} - \frac{xy^4}{12} + 2x + \frac{y^8}{576} - \frac{y^6}{72} < 0
\end{align}
$$
ですね。これは手計算で求めたくねえ。。。
手順3.図示
max_range = 3
delta = 0.025
xrange = np.arange(-max_range, max_range, delta)
yrange = np.arange(-max_range, max_range, delta)
X, Y = np.meshgrid(xrange,yrange)
# Figureを作成
fig = plt.figure(figsize=(5, 5))
# FigureにAxes(サブプロット)を追加
ax = fig.add_subplot(111)
#軸の設定
plt.axis([-max_range, max_range, -max_range, max_range])
plt.gca().set_aspect('equal', adjustable='box')
# 軸を中心の方に持っていく
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
ax.set_ylabel("$Im$",y = 1)
ax.set_xlabel("$Re$", x=1)
#描画
Z2 = (X**8)/576 + (X**7)/72 + (X**6)*(Y**2)/144 + 5*(X**6)/72 + (X**5)*(Y**2)/24 + (X**5)/4 + (X**4)*(Y**4)/96 + (X**4)*(Y**2)/8 + 2*(X**4)/3 + (X**3)*(Y**4)/24 + (X**3)*(Y**2)/6 + 4*(X**3)/3 + (X**2)*(Y**6)/144 + (X**2)*(Y**4)/24 + 2*(X**2) + X*(Y**6)/72 - X*(Y**4)/12 + 2*X + (Y**8)/576 - (Y**6)/72
plt.contour(X, Y, Z2, [0], colors='black', corner_mask=True)
plt.plot(X[Z2 < 0], Y[Z2<0], color='gray' ,alpha=0.5)
plt.savefig("./figure/rk4_stb.png")
plt.show()
出力は
ちゃんとできました。
まあ、この方法、$f(x,y)<0$にした後に、Zに直接、$f(x,y)$を入力してるのすごい脳筋な方法なんですけどね。
でも変に考えずに、こっちの方が早かったので...。アホなので。
最後に
珍しく連投となりましたが、これは早く片付けたかったので、連投も構わず、連投しました連投。
さて、数値解析のレポートも終わったし、試験勉強と、もう一つのレポートしなきゃ。まずい...！！！
俺ガイルも読みたいのじゃ〜。
では今日はここまで。
